Khái niệm đạo hàm là một trong những nền tảng cốt lõi của giải tích toán học, mở ra một kỷ nguyên mới cho sự phát triển của khoa học và kỹ thuật. Giống như Top 10 Nhôm Kính luôn tìm kiếm sự chính xác trong từng chi tiết, đây chính là công cụ để đo lường “tốc độ thay đổi” tức thời của vạn vật.
Đạo Hàm Là Gì? Định Nghĩa Và Ý Nghĩa Trực Quan Nhất
Trước khi đi vào các công thức phức tạp, việc hiểu rõ bản chất của đạo hàm là vô cùng quan trọng.
Định nghĩa chính xác theo giới hạn
Trong toán học, đạo hàm của một hàm số y = f(x) tại một điểm x₀, ký hiệu là f'(x₀) hoặc dy/dx, được định nghĩa là giới hạn của tỉ số giữa sự thay đổi của hàm số (Δy) và sự thay đổi của đối số (Δx) khi Δx tiến dần về 0. Công thức tổng quát: f'(x₀) = lim (Δx→0) [f(x₀ + Δx) – f(x₀)] / Δx Về bản chất, đạo hàm đo lường sự biến thiên (thay đổi) của hàm số tại một điểm cụ thể.
Ý nghĩa hình học: Hệ số góc của tiếp tuyến
Đây là cách hiểu trực quan và quan trọng nhất của đạo hàm. Giá trị của đạo hàm f'(x₀) chính là hệ số góc của đường tiếp tuyến với đồ thị hàm số y = f(x) tại điểm có hoành độ x₀.
- Nếu f'(x₀) > 0, tiếp tuyến dốc lên, hàm số đang đồng biến (tăng) tại x₀.
- Nếu f'(x₀) < 0, tiếp tuyến dốc xuống, hàm số đang nghịch biến (giảm) tại x₀.
- Nếu f'(x₀) = 0, tiếp tuyến nằm ngang, điểm x₀ là một điểm cực trị (cực đại hoặc cực tiểu) hoặc điểm uốn của đồ thị.
Ý nghĩa vật lý: Vận tốc tức thời và các đại lượng tức thời
Nếu một vật chuyển động có phương trình quãng đường theo thời gian là s = s(t), thì đạo hàm của quãng đường theo thời gian, s'(t), chính là vận tốc tức thời của vật tại thời điểm t. Tương tự, đạo hàm của vận tốc theo thời gian, v'(t), chính là gia tốc tức thời a(t). Mở rộng ra, đạo hàm còn được dùng để mô tả tốc độ của rất nhiều quá trình biến đổi trong vật lý, hóa học, kinh tế…
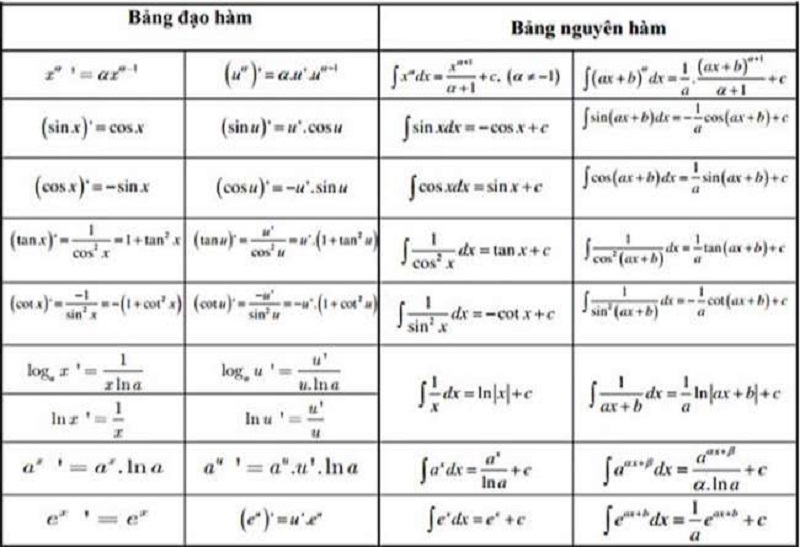
Bảng Công Thức Đạo Hàm Đầy Đủ Và Chi Tiết Nhất
Việc ghi nhớ các công thức cơ bản là yêu cầu bắt buộc để có thể giải quyết các bài toán liên quan đến đạo hàm.
1. Đạo hàm của các hàm số sơ cấp cơ bản
- Đạo hàm của hằng số: (C)’ = 0
- Đạo hàm của hàm số lũy thừa: (xⁿ)’ = n * xⁿ⁻¹
- Đạo hàm của căn bậc hai: (√x)’ = 1 / (2√x)
- Đạo hàm của 1/x: (1/x)’ = -1 / x²
2. Đạo hàm của các hàm số lượng giác
- (sin x)’ = cos x
- (cos x)’ = -sin x
- (tan x)’ = 1 / cos²x = 1 + tan²x
- (cot x)’ = -1 / sin²x = -(1 + cot²x)
3. Đạo hàm của các hàm số mũ và logarit
- Hàm số mũ cơ số e: (eˣ)’ = eˣ
- Hàm số mũ cơ số a: (aˣ)’ = aˣ * ln(a)
- Hàm logarit tự nhiên: (ln x)’ = 1/x
- Hàm logarit cơ số a: (logₐx)’ = 1 / (x * ln a)
4. Các quy tắc tính đạo hàm
Giả sử u = u(x) và v = v(x) là các hàm số có đạo hàm:
- Tổng/Hiệu: (u ± v)’ = u’ ± v’
- Tích: (u * v)’ = u’v + uv’
- Tích với hằng số: (k * u)’ = k * u’
- Thương: (u/v)’ = (u’v – uv’) / v²
5. Công thức đạo hàm của hàm số hợp (y = f(u(x)))
Đây là công thức quan trọng nhất, được áp dụng trong hầu hết các bài toán phức tạp. Quy tắc chuỗi (Chain Rule): y’ₓ = y’ᵤ * u’ₓ
Bảng công thức mở rộng cho hàm hợp:
- (uⁿ)’ = n * uⁿ⁻¹ * u’
- (√u)’ = u’ / (2√u)
- (sin u)’ = (cos u) * u’
- (cos u)’ = -(sin u) * u’
- (eᵘ)’ = eᵘ * u’
- (ln u)’ = u’ / u
5 Ứng Dụng Quan Trọng Nhất Của Đạo Hàm Trong Toán Học Và Thực Tiễn
Sức mạnh của đạo hàm không chỉ nằm ở lý thuyết mà còn ở khả năng ứng dụng vô cùng rộng rãi.
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số
Đây là ứng dụng trực tiếp và quen thuộc nhất với học sinh. Bằng cách xét dấu của đạo hàm cấp một (f'(x)), chúng ta có thể xác định được các khoảng đồng biến, nghịch biến và các điểm cực trị (cực đại, cực tiểu) của hàm số. Kết hợp với đạo hàm cấp hai (f”(x)) để tìm điểm uốn và xét tính lồi, lõm, chúng ta có thể phác họa được chính xác hình dạng của đồ thị hàm số.
2. Viết phương trình tiếp tuyến của đồ thị hàm số
Dựa vào ý nghĩa hình học, việc viết phương trình tiếp tuyến trở nên đơn giản. Phương trình tiếp tuyến của đồ thị y = f(x) tại điểm M(x₀, y₀) có dạng: y – y₀ = f'(x₀) * (x – x₀) Trong đó, f'(x₀) chính là hệ số góc của tiếp tuyến. Đây là dạng toán cơ bản và thường xuyên xuất hiện trong các kỳ thi.
3. Tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN)
Ứng dụng này có ý nghĩa thực tiễn rất lớn. Bằng cách tìm các điểm cực trị (nơi đạo hàm bằng 0 hoặc không xác định) và so sánh giá trị của hàm số tại các điểm đó với giá trị tại hai đầu của một khoảng cho trước, chúng ta có thể tìm được GTLN và GTNN. Trong kinh tế, nó được dùng để tối ưu hóa lợi nhuận, tối thiểu hóa chi phí. Trong kỹ thuật, nó được dùng để tìm ra các thông số tối ưu cho một thiết kế.
4. Giải quyết các bài toán vật lý và kỹ thuật
Như đã đề cập, đạo hàm là công cụ không thể thiếu để mô tả các đại lượng tức thời. Nó được dùng để tính toán vận tốc, gia tốc trong chuyển động; cường độ dòng điện tức thời trong mạch điện xoay chiều; tốc độ phản ứng trong hóa học… Hầu hết các định luật vật lý vi phân đều được biểu diễn dưới dạng các phương trình chứa đạo hàm.
5. Ứng dụng trong kinh tế và tài chính
Trong kinh tế học, các khái niệm như “chi phí biên”, “doanh thu biên”, “năng suất biên” thực chất chính là đạo hàm của hàm chi phí, hàm doanh thu, hàm sản xuất. Ví dụ, chi phí biên (MC) là đạo hàm của tổng chi phí (TC), cho biết chi phí tăng thêm khi sản xuất thêm một đơn vị sản phẩm. Các nhà kinh tế sử dụng công cụ này để đưa ra các quyết định tối ưu về sản lượng và giá cả.

Các Dạng Bài Tập Thường Gặp Và Phương Pháp Giải
Nắm vững phương pháp giải cho từng dạng bài là chìa khóa để đạt điểm cao.
Dạng 1: Tính đạo hàm bằng định nghĩa
Phương pháp: Áp dụng trực tiếp công thức giới hạn. Dạng này thường dùng để kiểm tra sự hiểu biết về bản chất của đạo hàm, ít xuất hiện trong các bài toán phức tạp. Cần nắm vững các kỹ thuật khử dạng vô định 0/0.
Dạng 2: Tính đạo hàm bằng công thức
Phương pháp: Đây là dạng phổ biến nhất. Học sinh cần thuộc lòng bảng công thức đạo hàm của các hàm số cơ bản và các quy tắc tính. Kỹ năng nhận dạng hàm số (đâu là hàm hợp, hàm tích, hàm thương…) là rất quan trọng. Luôn nhớ nhân với u’ khi tính đạo hàm của hàm hợp.
Dạng 3: Viết phương trình tiếp tuyến
Phương pháp:
- Bài toán 1: Tại một điểm M(x₀, y₀) cho trước. Tính y’ = f'(x), sau đó tính f'(x₀). Áp dụng công thức y – y₀ = f'(x₀) * (x – x₀).
- Bài toán 2: Biết hệ số góc k. Giải phương trình f'(x) = k để tìm hoành độ tiếp điểm x₀. Từ đó tìm y₀ và viết phương trình.
- Bài toán 3: Tiếp tuyến đi qua một điểm A(x₁, y₁) cho trước. Gọi M(x₀, y₀) là tiếp điểm. Viết phương trình tiếp tuyến tại M. Thay tọa độ điểm A vào phương trình đó để giải ra x₀.
Dạng 4: Ứng dụng đạo hàm để giải phương trình, bất phương trình
Phương pháp: Sử dụng tính đơn điệu của hàm số. Xét hàm số y = f(x). Tính f'(x) và chứng minh f(x) luôn đồng biến hoặc nghịch biến trên một tập xác định. Từ đó suy ra phương trình f(x) = k có không quá một nghiệm. Kỹ thuật này rất hữu ích để giải quyết các phương trình phức tạp.
Dạng 5: Bài toán thực tế tìm GTLN, GTNN
Phương pháp:
- Bước 1: Dựa vào các dữ kiện của bài toán, xây dựng một hàm số một biến biểu thị cho đại lượng cần tối ưu (ví dụ: hàm lợi nhuận P(x), hàm chi phí C(x)…).
- Bước 2: Xác định tập xác định (điều kiện) của biến số đó.
- Bước 3: Sử dụng đạo hàm để tìm GTLN hoặc GTNN của hàm số trên tập xác định đã tìm.
- Bước 4: Kết luận bài toán.
Mối Liên Hệ Giữa Đạo Hàm Và Tích Phân
Đạo hàm và tích phân là hai khái niệm ngược nhau, chúng là hai mặt của cùng một đồng xu, được kết nối bởi Định lý cơ bản của giải tích.
Nguyên hàm – Phép toán ngược của đạo hàm
Nếu hàm số F(x) có đạo hàm là F'(x) = f(x), thì F(x) được gọi là một nguyên hàm của f(x). Tích phân bất định của f(x), ký hiệu là ∫f(x)dx, chính là đi tìm họ tất cả các nguyên hàm của f(x).
Định lý cơ bản của giải tích
Định lý này phát biểu rằng, nếu f là một hàm liên tục trên đoạn [a, b], thì tích phân xác định của f từ a đến b có thể được tính bằng cách lấy F(b) – F(a), trong đó F là một nguyên hàm bất kỳ của f. Mối liên hệ này đã thống nhất hai nhánh lớn của giải tích là phép tính vi phân (đạo hàm) và phép tính tích phân.
Kết luận
Từ việc mô tả độ dốc của một con đường đến việc tối ưu hóa lợi nhuận trong kinh doanh, đạo hàm là một công cụ toán học vạn năng và đầy quyền lực. Top 10 Nhôm Kính tin rằng, việc nắm vững khái niệm này không chỉ giúp học sinh vượt qua các kỳ thi, mà còn mở ra một cách tư duy logic để phân tích và giải quyết các vấn đề trong thế giới thực.
